비방향성 그래프, 방향성 그래프 변환
지금까지의 확률 분포를 표현하기 위해, 방향성 그래프와 비방향성 그래프를 조사하였다. 이제 두 그래프의 관련성에 대해 살펴봐요. 먼저 방향성 그래프를 사용하여 지정된 모델을 비방향성 그래프로 변환합니다. 첫 번째 예로 다음을 생각해 봅시다.
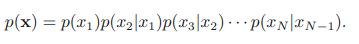
이것을 그래프로 표현하면 다음과 같다.
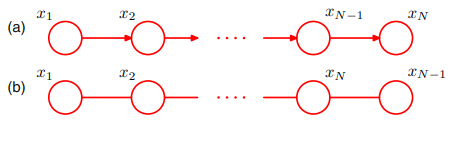
이 비방향성 그래프에서, 최대 크릭은 단순히 인접한 노드 쌍에 대응하기 때문에, 전술한 바와 같이 비방향성 그래프가 표현되었다. 이것을 결합 분포로 다음과 같이 확인할 수 있다.
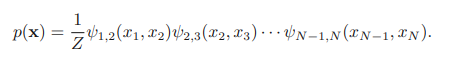
여기서, 각 포텐셜 함수는 다음과 같이 정의된다.
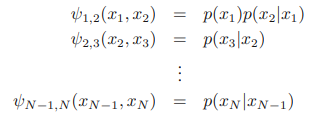
이와 같이, 방향성 그래프의 조건부 확률을 비방향성 그래프의 크릭 활성화 함수와 일치시킬 수 있으면 변환이 가능하다. 역도 마찬가지다. 이를 충족하기 위해 각 조건부 분포에서 발견되는 변수 세트는 비방향 그래프의 클릭 중 적어도 하나에 속해야 합니다. 이것은 방향 그래프에 하나의 부모가 있는 경우(머리에서 꼬리 또는 꼬리에서 꼬리까지), 방향성 링크를 비방향성으로 변경하기만 하면 됩니다. 그러나 머리에서 머리까지의 경로를 가진 노드에서는 그렇지 않습니다. 다음 결합 분포를 살펴 보겠습니다.
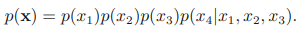
상기 결합 분포를 방향성 그래프 및 비방향성 그래프로 나타낸다.
위의 조건부 분포를 크릭 포텐셜 함수에 흡수하려면 4개의 변수를 모두 하나의 크릭에 포함시켜야 합니다. 따라서 x4의 모든 부모를 링크로 연결해야 합니다.이러한 프로세스 도덕화라고 불리며 결과에 해당하는 비방향 그래프를 도덕적 그래프라고 부른다.
따라서 상위 노드를 비방향성 링크로 연결해야 하는 이유는 조건부 독립성으로도 이해할 수 있습니다. 방향 그래프 (a)는 머리 대 두부 노드이다. x4가 관찰되면 x1, x2, x3은 서로 조건부 독립성을 충족시키지 못함알고있다 (조건부 독립 (conditional independence) (tistory.com)). 이제 (b)를 보자.방향성 그래프에서 비방향성 그래프로 변환하는 과정에서 상위 노드가 링크로 연결되어 있지 않다고 가정합니다. 그렇다면 x4가 관찰되면 x1, x2, x3은 서로 x4를 통과하지 않고 연결되지 않습니다.이것은 비방향성 그래프의 조건부 독립 조건에 해당합니다.(마르코 프랜덤 필드 (Markov random field) (tistory.com)). 즉, 이 경우, 방향성 그래프일 때는 조건부 독립성질을 나타내지 않지만, 비방향성 그래프로 변환한 결과 조건부 독립성질을 띄는 모순이 생긴다. 이것은 동일한 확률 분포를 나타내지 않음을 의미합니다. 따라서, 변환시에 부모 노드를 비방향성 링크로 접속하여, x4가 관측되어도 x1, x2, x3이 서로 x4를 통과하지 않고 접속되도록 해야 하는 것이다.
따라서 결론은 방향성 그래프를 비방향성 그래프로 변환하기 위해 먼저 각 노드의 상위 노드의 모든 쌍 사이에 비방향성 링크를 추가한 다음 모든 링크의 방향 표시를 제거합니다. 도덕적 그래프를 만들어야합니다. 그런 다음 방향 그래프의 조건 분포를 하나씩 취하고 크릭 포텐셜 중 하나에 곱하면 변환이 완료됩니다.
따라서 방향성 그래프를 비방향성 그래프로 변환하는 과정은 접합 트리 알고리즘과 같은 추론 기술에서 중요한 역할을 한다.
방향성 그래프와 비방향성 그래프의 차이
방향성 그래프와 비방향성 그래프가 조건부 독립성을 나타내는 방법이 다르다는 것을 이전 기사를 통해 조사하였다. 그런데 각 그래프는 모든 조건부 독립성을 표현할 수는 없습니다. 두 그래프를 각각 표현할 수 없는 조건부 독립성이 다릅니다.
이에 앞서 먼저 D사상, I사상, 완벽사상에 대해 살펴봐요.
- D사상는 특정 분포의 조건부 독립성이 그래프에 모두 반영되는 경우입니다. 예를 들어, 링크가 없는 (완전히 연결이 끊긴) 그래프는 모든 노드가 조건부 독립이므로 D 생각에 해당합니다.
- I사상그래프가 나타내는 모든 조건부 독립성이 분포의 조건부 독립성에 포함되는 경우입니다. 예를 들어, 완전하게 연결된 그래프는 조건부 독립성을 갖지 않으므로 I 사상에 대응한다.
- 완벽한 사상는 D사상이면서 I사상인 그래프이다. 즉, 특정 분포의 조건부 독립성이 그래프에 모두 반영되고, 그래프가 나타내는 조건부 독립성이 해당 분포의 조건부 독립성에 포함되는 경우이다.
이것을 조금 간단하게 설명하기 위해, 어떤 분포와 그 분포를 그래프로 나타낸 것을 생각해 봅시다. 그리고 각각이 가지고 있는 조건부 독립 성질을 생각해 보자.
D사상은 다음과 같다.
분포—-조건부 독립—->그래프
즉, 분포가 갖는 모든 조건부 독립 특성이 그래프에 반영된 상태이다.
I 생각은 다음과 같다.
분포<----조건부 독립----그래프
즉, 그래프가 갖는 모든 조건부 독립 특성이 분포에 반영된 상태이다.
완벽한 사상은 다음과 같습니다.
분포<----条件付独立---->그래프
분포가 갖는 조건부 독립 특성과 그래프가 갖는 조건부 독립 특성은 완전히 일치한다.
이러한 개념을 바탕으로 우리의 논의를 “방향/비방향 그래프가 완전한 사상을 제공하는 분포는 어떻게 다른가”라고 정의하자. 이것은 반다이어그램으로 나타낼 수 있습니다.
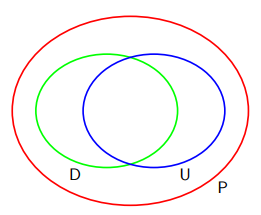
위의 반다이어그램과 같이 방향성 그래프는 완전 사상이 가능하지만, 비방향성 그래프는 완전 사상이 불가능한 경우(교차 집합을 제외한 D)가 존재하고, 이것과 반대인 경우(교차 집합 를 제외한 U)도 존재한다. 또한, 양 그래프 모두 완벽 사상이 가능해도(교집합), 양 그래프 모두 완벽 사상이 불가능(D와 U의 합집합의 여집합)이어도 된다. 이것의 몇 가지 예를 살펴 보겠습니다.
다음 그래프를 생각해 봅시다.
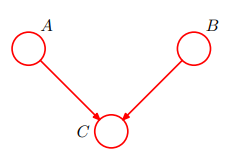
위의 방향 그래프는 다음을 포함합니다.
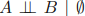
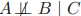
동일한 세 변수에 대해 완전히 생각하는 비방향성 그래프는 없습니다.
이번에는 다른 그래프를 생각해 봅시다.
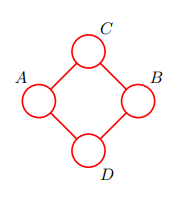
상기 비방향성 그래프는 다음을 포함한다.
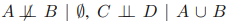
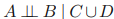
같은 네 개의 변수에 대해 완전히 생각하는 방향 그래프는 없습니다.
